Redis的ZSet数据结构

ZSet的两种“面孔”：紧凑与高效

与Hash类型相似，一个ZSet对象也会根据存储数据的大小和数量，在两种编码方式之间进行选择。

紧凑编码：当ZSet中存储的元素数量较少，且每个元素的成员（member）长度都较短时，Redis会采用一种极其节省内存的连续存储结构。
- Redis 6及之前: ziplist (压缩列表)
- Redis 7之后: listpack (紧凑列表)
高效编码：一旦超出预设的阈值，ZSet就会被转换为skiplist（跳表）+ dict（字典）的复合结构。

这个转换的“门槛”由两个参数共同决定：

zset-max-ziplist-entries / zset-max-listpack-entries: 紧凑编码下允许的最大元素数量（默认128）。
zset-max-ziplist-value / zset-max-listpack-value: 紧凑编码下每个成员（member）的最大长度（默认64字节）。

# Redis 6中的配置
127.0.0.1:6379> config get zset-max-ziplist-*
1) "zset-max-ziplist-entries"
2) "128"
3) "zset-max-ziplist-value"
4) "64"

# Redis 7中的配置 (同时保留ziplist以兼容)
127.0.0.1:6379> config get zset-max-*-*
1) "zset-max-listpack-value"
2) "64"
3) "zset-max-ziplist-value"
4) "64"
5) "zset-max-ziplist-entries"
6) "128"
7) "zset-max-listpack-entries"
8) "128"

只要任一条件不满足，ZSet就会从紧凑编码自动升级为skiplist。这种升级同样是单向的，不可逆。

编码转换实战

Redis 6 (ziplist ) :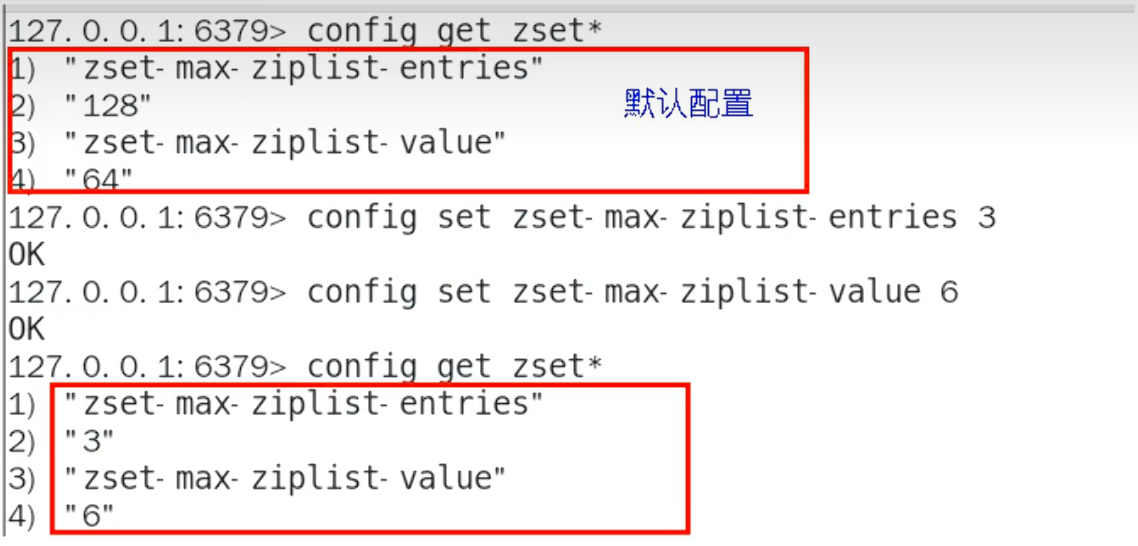
当添加的成员长度超过6字节时，编码自动转换为skiplist。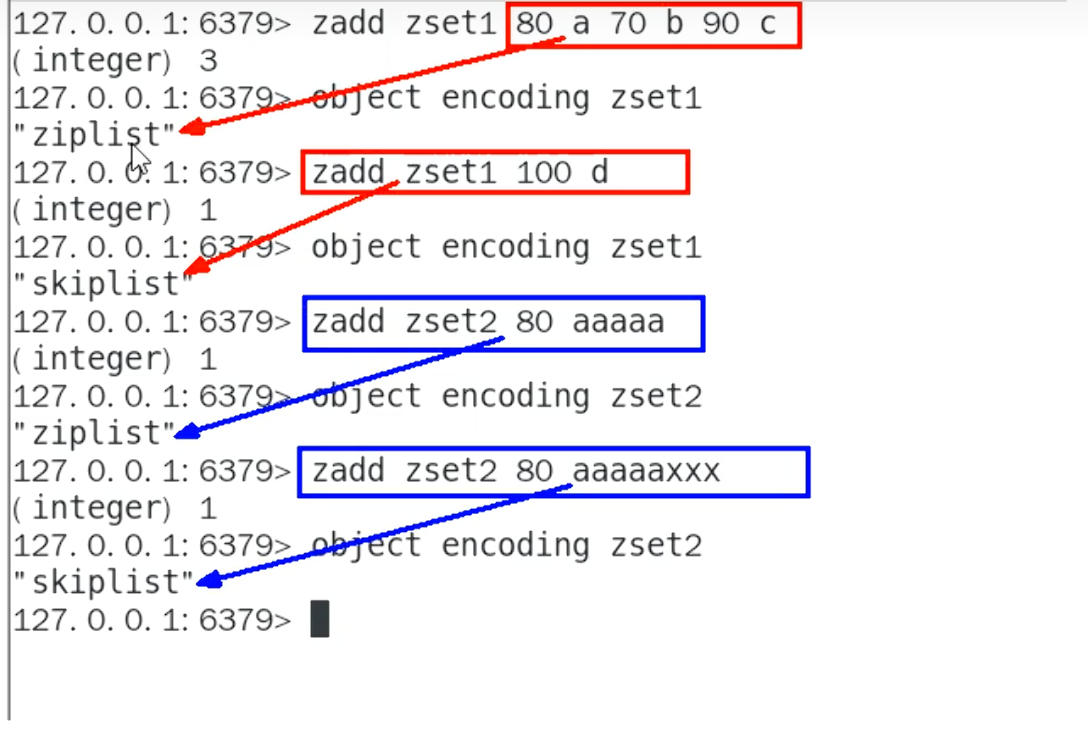
Redis 7 (listpack ) :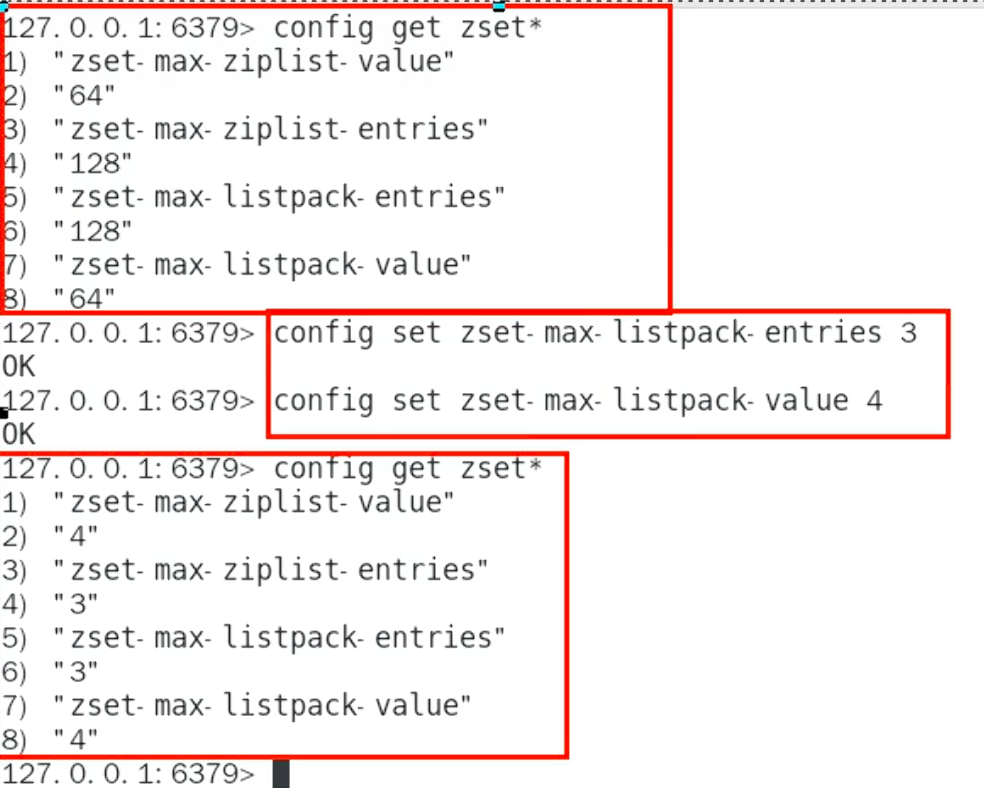
当元素数量超过4个时，编码自动转换为skiplist。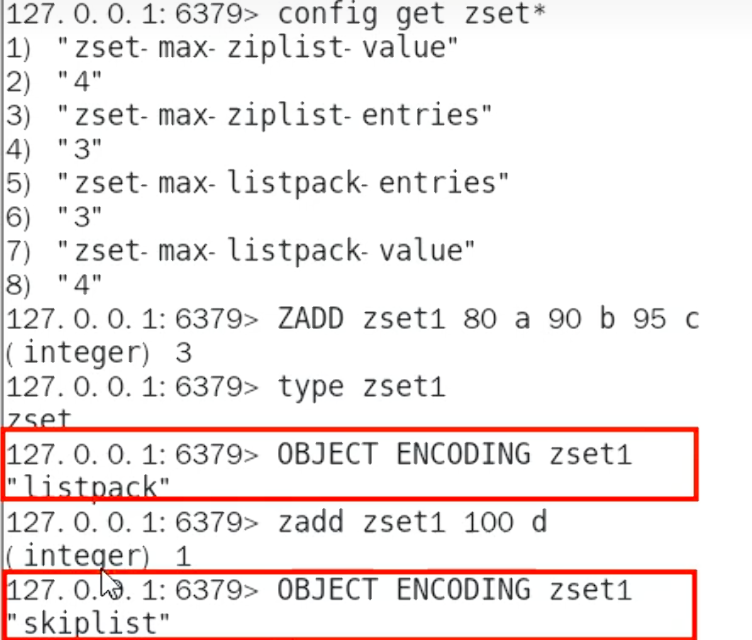

从zaddCommand的源码调用栈中，我们也能清晰地看到，当对象编码为OBJ_ENCODING_LISTPACK时，会进入特定的处理分支，并在不满足条件时触发转换。

zadd源码逻辑

为何需要跳表？

当数据量增大，ziplist/listpack这种O(N)查找效率的线性结构显然无法满足性能要求。我们需要一种更高效的有序结构。

普通有序链表：查找一个元素，最坏情况下需要遍历整个链表，时间复杂度为O(N)。
引入“索引” ：为了加速查找，我们可以借鉴数据库索引的思想，从原始链表中提取出部分节点，形成一级“快速通道”或“索引”。
多级索引的诞生：如果一层索引不够快，我们可以在索引之上再建立索引，层层向上，最终形成一个多级的索引结构。这就是跳表 (Skip List) 。

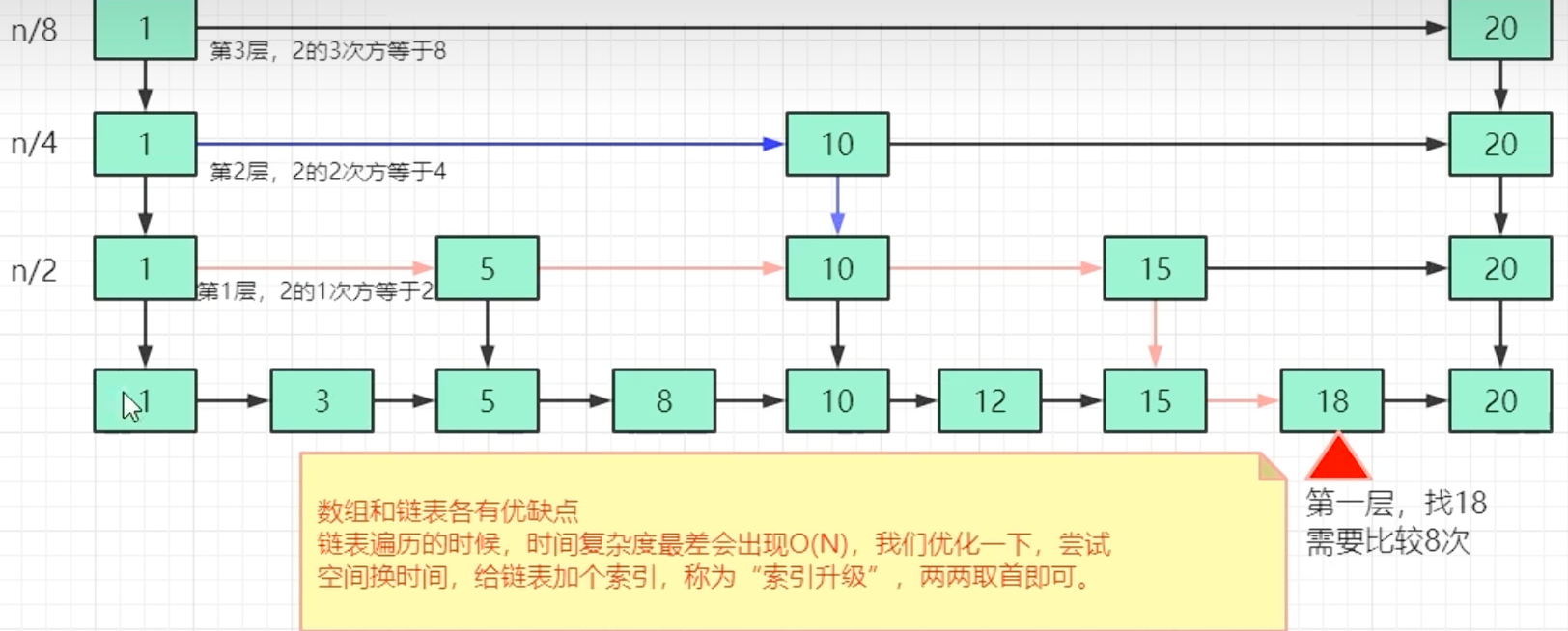
跳表，本质上是“支持二分查找的链表”，它通过构建多级索引，实现了空间与时间的完美平衡。

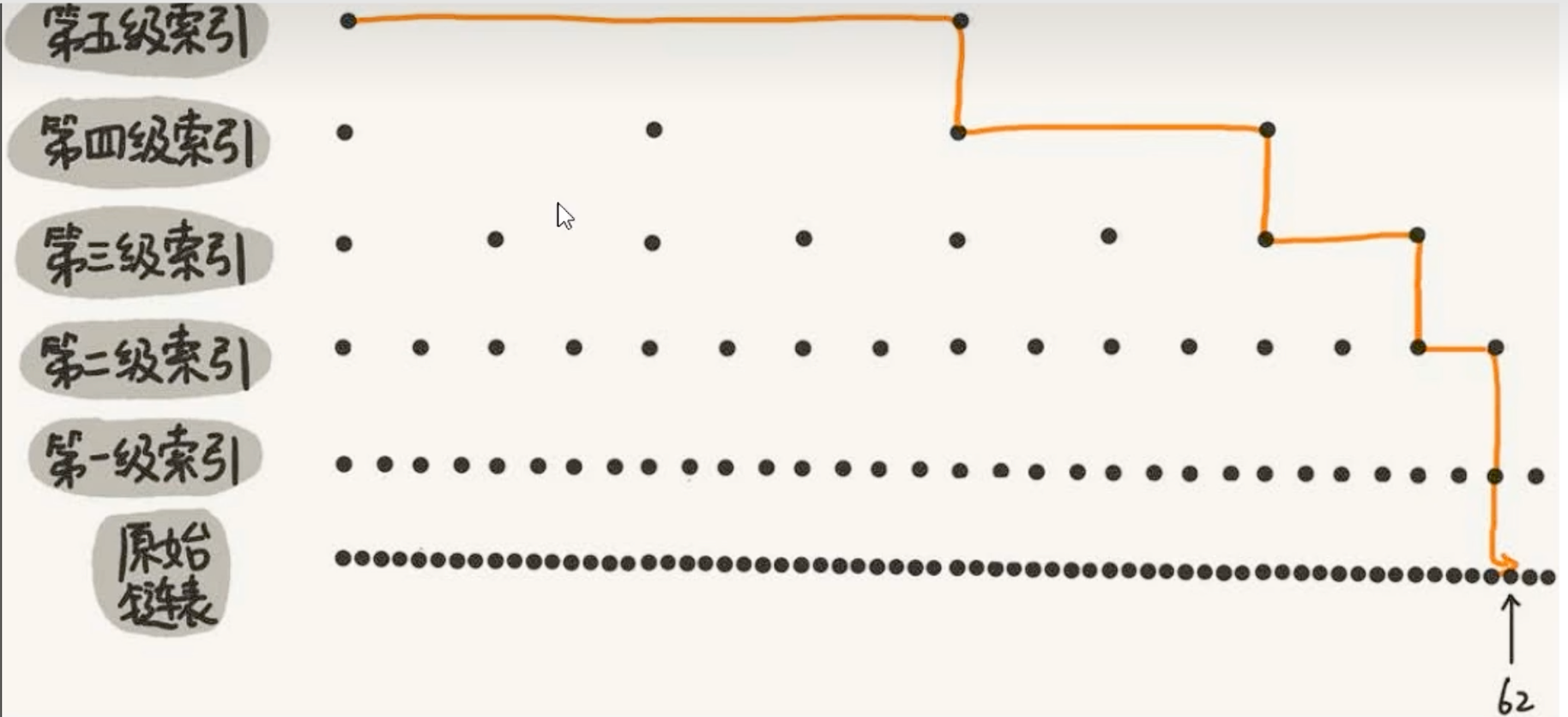
64个节点的跳表示例

如上图，在一个包含64个节点的跳表中查找第62个元素，不再需要62次遍历，而只需沿着最高层索引“跳跃”，逐层向下逼近，效率大大提升。

时空复杂度分析

时间复杂度: 假设每2个节点提取一个索引，那么k级索引的节点数约为n/(2^k)。整个跳表的高度约为log₂n。在每一层索引中，遍历的节点数不超过3个。因此，跳表的查找、插入、删除的时间复杂度都是O(logN) 。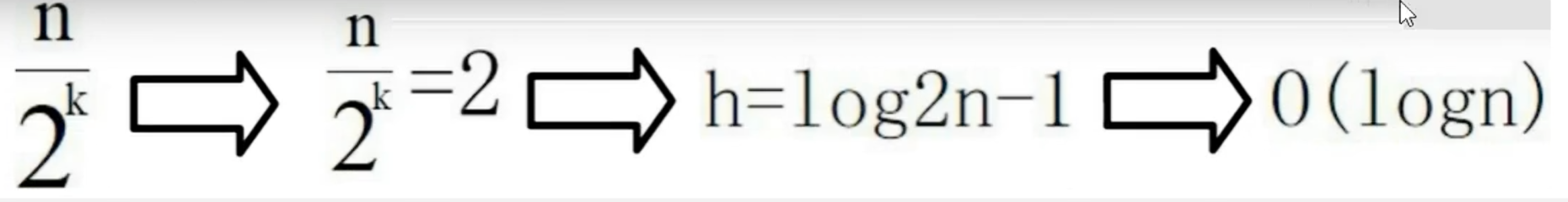
空间复杂度: 同样假设每2个节点提取一个索引，总的索引节点数约为 n/2 + n/4 + n/8 + ... + 2 ≈ n。因此，跳表的空间复杂度是O(N) 。虽然增加了额外的存储开销，但换来的是查询效率的巨大飞跃。

`skiplist`的插入与删除操作（含源码逻辑）

跳表的动态维护是其设计的精髓所在。

插入操作

查找插入位置: 插入操作首先需要像查找操作一样，从最高层索引开始，找到每一层应该插入新节点的位置。在这个过程中，我们会记录下每一层需要插入位置的前驱节点（保存在一个update数组中）。
随机决定新节点层高: 这是跳表的随机化核心。新节点会被插入到多少层索引中，是通过一个随机算法决定的。Redis的实现是：新节点有1/P（默认P=4，即25%）的概率增加一层，直到达到最大层高。这种概率性设计，使得跳表在动态增删后，能大概率地维持其结构平衡，而无需像平衡树那样进行复杂的旋转操作。
创建并插入新节点: 创建一个具有随机出的层高的新节点。
逐层更新指针: 遍历update数组，从第0层到新节点的最高层，将被记录的前驱节点的forward指针指向新节点，并将新节点的forward指针指向原前驱节点的后继节点，完成链入操作。

源码逻辑 (zslInsert ) :

目标：在一个现有的跳表中，插入一个新节点 {score: 21, value: "V21"}。

Level 2: H ------------------------------> 37
         |                                  |
Level 1: H ------> 13 -------------------->37
         |        	|                       |
Level 0: H -> 9 -> 13 -> 17 -> 26 -> 30 -> 37 -> 42‍

步骤1：查找插入路径并记录前驱节点 (`update`数组)

这个过程就像一次查找，我们需要从最高层开始，为每一层找到新节点应该插入的位置，并记录下该位置的前驱节点。

Level 2: 从 H 开始，H->forward 是 37。21 < 37，所以 21 应该在 H 和 37 之间。记录 Level 2 的前驱节点是 H。update[2] = H。
Level 1: 从 H 开始，H->forward 是 13。21 > 13，前进。当前节点是 13，13->forward 是 37。21 < 37，所以 21 应该在 13 和 37 之间。记录 Level 1 的前驱节点是 13。update[1] = 13。
Level 0: 从 13 开始（上一层的终点），13->forward 是 17。21 > 17，前进。当前节点是 17，17->forward 是 26。21 < 26，所以 21 应该在 17 和 26 之间。记录 Level 0 的前驱节点是 17。update[0] = 17。

源码逻辑 (zslInsert ) :

// t_zset.c
// 1. 查找路径记录:
//    update[] 数组记录每层的前驱节点
zskiplistNode *update[ZSKIPLIST_MAXLEVEL], *x;
int i;

x = zsl->header; // 从头节点开始
for (i = zsl->level-1; i >= 0; i--) { // 从最高层向下
    // 在当前层循环查找，直到找到插入位置的前一个节点
    while (x->level[i].forward &&
            (x->level[i].forward->score < score ||
                (x->level[i].forward->score == score &&
                 sdscmp(x->level[i].forward->ele, ele) < 0)))
    {
        x = x->level[i].forward; // 前进
    }
    update[i] = x; // 记录这一层的前驱节点
}

步骤2 & 3：随机层高并创建新节点

通过随机算法，假设我们为新节点“掷”出的层高为 2。这意味着新节点将出现在 Level 0 和 Level 1 中。然后，我们创建一个层高为2的新节点 (21)。

源码逻辑 (zslInsert ) :

// 2. 随机层高:
//    zslRandomLevel() 通过概率决定新节点的层高
int level = zslRandomLevel();

// 3. 如果新层高大于当前跳表最大层高，扩展跳表
if (level > zsl->level) { /* ... */ }

// 4. 创建新节点
x = zslCreateNode(level, score, ele);

逐层更新指针

现在，我们利用之前记录的update数组来“接入”新节点。

Level 0: update[0] 是 17。
- 将 (21) 的 forward[0] 指向 17 原来的 forward[0] (即 26)。
- 将 17 的 forward[0] 指向新节点 (21)。
Level 1: update[1] 是 13。
- 将 (21) 的 forward[1] 指向 13 原来的 forward[1] (即 37)。
- 将 13 的 forward[1] 指向新节点 (21)。

可视化结果：

Level 2: H ------------------------------> 37
         |                                 |
Level 1: H ------> 13 ------> 21 --------> 37
         |          |          |           |
Level 0: H -> 9 -> 13 -> 17 -> 21 -> 26 -> 37 -> 42

源码逻辑 (zslInsert ) :

// 5. 逐层更新指针:
for (i = 0; i < level; i++) {
    // 新节点的forward指针指向前驱节点原来的forward
    x->level[i].forward = update[i]->level[i].forward;
    // 前驱节点的forward指针指向新节点
    update[i]->level[i].forward = x;
}

‍

删除操作

查找目标节点: 与插入类似，首先查找到要删除的节点，并记录下其在每一层的前驱节点（同样保存在update数组中）。
逐层更新指针 (“绕过”操作) : 遍历每一层，如果该层包含目标节点，就将被记录的前驱节点的forward指针，直接指向目标节点的后继节点，从而将目标节点从该层“链”中移除。
释放节点: 在所有层都完成“绕过”操作后，释放目标节点的内存。
更新跳表层高: 如果删除的是最高层的最后一个节点，可能需要降低跳表的总层高。

目标：从上述跳表中，删除节点 {score: 21, value: "V21"}。

步骤1：查找目标节点并记录前驱

和插入一样，我们首先要找到每一层中待删除节点的前驱节点，并存入update数组。结果与插入时的查找过程完全相同：update[2]=H, update[1]=13, update[0]=17。

步骤2：逐层更新指针 (“绕过”操作)

现在，我们逐层修改指针，将被删除节点“架空”。

Level 0: update[0] 是 17。它的 forward[0] 正是我们要删除的节点 (21)。
- 我们将 17 的 forward[0] 指向 (21) 的 forward[0] (即 26)。
Level 1: update[1] 是 13。它的 forward[1] 正是我们要删除的节点 (21)。
- 我们将 13 的 forward[1] 指向 (21) 的 forward[1] (即 37)。
Level 2: update[2] 是 H。它的 forward[2] 是 37，不是 (21)，所以这一层无需操作。

可视化结果：

Level 2: H ----------------------------- > 37
         |                                 |
Level 1: H ------> 13 -------------------> 37
         |         |                       |
Level 0: H -> 9 -> 13 -> 17 -> 26 -> 30 -> 37 -> 42

步骤3：释放节点

在所有指针都更新完毕后，节点 (21) 已经不再被任何forward指针引用，可以安全地释放其内存。

源码逻辑 (zslDelete -> zslDeleteNode ) :

// t_zset.c
void zslDeleteNode(zskiplist *zsl, zskiplistNode *x, zskiplistNode **update) {
    int i;
    // 1. 逐层更新指针:
    for (i = 0; i < zsl->level; i++) {
        // 如果前驱节点的下一个是目标节点x
        if (update[i]->level[i].forward == x) {
            // 将前驱节点直接指向目标节点的后继节点，完成“绕过”
            update[i]->level[i].forward = x->level[i].forward;
        }
    }
    // ...
    // zslFreeNode(x) 会在 zslDelete 中被调用
}

‍

更新操作 (Update)

skiplist本身没有独立的“更新”操作。当需要更新一个元素的分数（score）时，Redis采用了一种更简单、更健壮的策略：

更新 = 删除旧节点 + 插入新节点

为什么这样做？

代码复用与健壮性：DELETE和INSERT是经过充分测试的核心操作，复用它们可以避免编写一套全新的、复杂的节点“移动”逻辑，降低了出错风险。
性能可接受：由于删除和插入操作的时间复杂度都是O(logN)，所以整个更新操作的时间复杂度也是O(logN)，性能完全在可接受的范围内。
dict的辅助：ZSet的skiplist编码总是与一个dict（字典）并存的。当需要更新时，可以通过dict以O(1)的效率快速找到旧分数和节点指针，为DELETE操作提供了极大的便利。

结论

ZSet的底层实现是Redis在内存效率与时间效率之间进行权衡的又一典范。

在数据量小、内容短的场景下，它采用ziplist/listpack，以时间换空间，追求极致的内存利用率。
当数据增长到一定规模，它果断“升级”为skiplist，以空间换时间，通过巧妙的多级索引结构，提供了对数级的、可预测的高性能有序操作。

skiplist以其相对简单（相比平衡树）的实现，和优雅的随机化平衡策略，成为了ZSet高性能的核心引擎，也是Redis设计哲学中实用主义与性能并重的完美体现。

Redis的ZSet数据结构

ZSet的两种“面孔”：紧凑与高效

编码转换实战

为何需要跳表？

时空复杂度分析

`skiplist`的插入与删除操作（含源码逻辑）

插入操作

步骤1：查找插入路径并记录前驱节点 (`update`数组)

步骤2 & 3：随机层高并创建新节点

逐层更新指针

删除操作

步骤1：查找目标节点并记录前驱

步骤2：逐层更新指针 (“绕过”操作)

步骤3：释放节点

更新操作 (Update)

结论

相关文章

cpu和io交互过程

内核态vs用户态

操作系统启动流程简介

操作系统的作用

ReentrantReadWriteLock

sychronized与锁升级

Redis的ZSet数据结构

ZSet的两种“面孔”：紧凑与高效

编码转换实战

为何需要跳表？

时空复杂度分析

​skiplist​​的插入与删除操作（含源码逻辑）

插入操作

步骤1：查找插入路径并记录前驱节点 (​​update​​数组)

步骤2 & 3：随机层高并创建新节点

逐层更新指针

删除操作

步骤1：查找目标节点并记录前驱

步骤2：逐层更新指针 (“绕过”操作)

步骤3：释放节点

更新操作 (Update)

结论

相关文章

cpu和io交互过程

内核态vs用户态

操作系统启动流程简介

操作系统的作用

ReentrantReadWriteLock

sychronized与锁升级

`skiplist`的插入与删除操作（含源码逻辑）

步骤1：查找插入路径并记录前驱节点 (`update`数组)