在海量数据处理中,我们经常面临一个看似简单却极具挑战性的问题:如何快速、准确地判断一个元素是否存在于一个庞大的集合中?
大厂的真实面试题:问题的提出
让我们从一个经典的面试场景开始:
面试官: 现有50亿个电话号码的记录,再给你10万个号码,如何快速准确地判断这10万个号码是否在那50亿的记录中?
让我们分析一下常规思路的局限性:
- 数据库查询:将50亿条记录存入数据库,然后对10万个号码进行逐一查询。即便有索引优化,面对海量的读操作,想要实现“快速”依然非常困难,对数据库的压力也是巨大的。
- 内存集合:将50亿个号码预加载到内存中的哈希集合(如
HashSet)中,查询效率确实能达到 O(1)。但我们来算一下空间成本:假设一个电话号码用64位长整型(8字节)存储,50亿个号码就需要50亿 * 8字节 = 40GB的内存。对于大多数服务器来说,这是一个难以承受的巨大开销。
既然传统方法行不通,我们需要一种更巧妙的、在空间和时间上都更高效的解决方案。
布隆过滤器(Bloom Filter)
布隆过滤器是1970年由Burton Howard Bloom提出的,它是一种空间效率极高的概率型数据结构,专门用于解决“一个元素是否在一个集合中”的问题。
核心思想:
它不存储元素本身,而是通过一个位数组(bit array) 和多个哈希函数(hash functions) 来标记元素的存在。
工作原理:
初始化:一个长度为
m的位数组,所有位都初始化为0。以及k个不同的哈希函数。
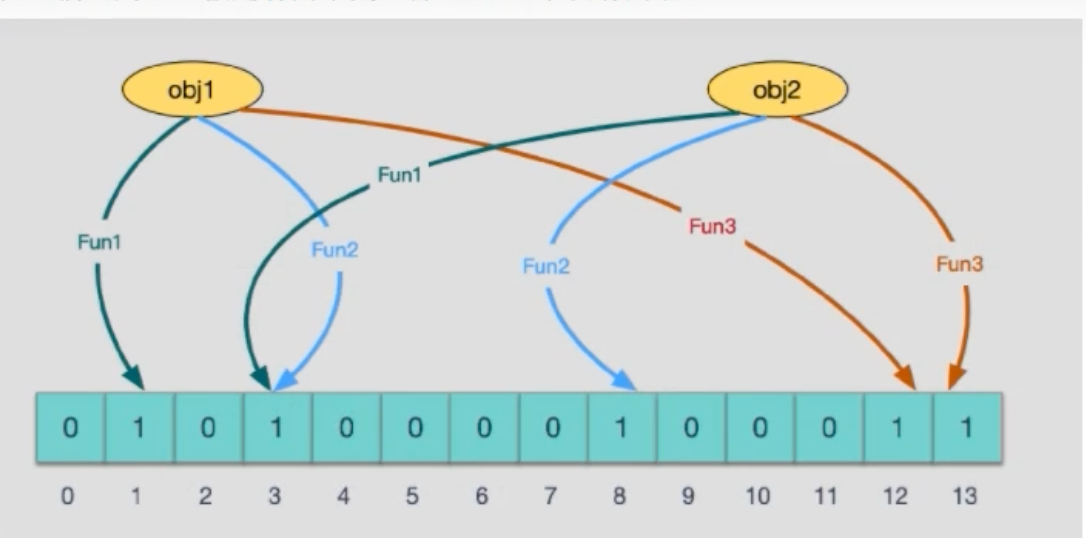
添加元素(add) :
- 当一个元素
key需要被添加到集合时,使用k个哈希函数分别对key进行计算,得到k个整数索引值。 - 将位数组中这
k个索引对应的位置置为1。
- 当一个元素
查询元素(query) :
- 当需要判断元素
key是否存在时,同样用k个哈希函数计算出k个索引位置。 - 检查位数组中这些位置的值。
- 如果其中任何一位是
0,那么这个key绝对不存在于集合中。 - 如果所有位都是
1,那么这个key可能存在于集合中。
- 当需要判断元素
关键特性:不完美的答案
布隆过滤器最独特的特性在于它的不确定性,这也是其空间效率的来源:
- 不存在时,判断绝对准确:如果一个元素从未被添加,那么它对应的某些哈希位必然是0。所以,当查询结果为“不存在”时,它是100%可信的。
- 存在时,判断可能错误(误判) :为什么说“可能存在”?因为哈希函数存在碰撞的可能。完全不同的两个元素,经过哈希计算后,可能会将同一个位标记为1。如下图所示,元素"Anonymity"和"Google"都将3号位标记为了1。如果此时我们查询一个从未添加过的元素,但它恰好也被哈希到这几个已经为1的位置,过滤器就会误判它“存在”。这就是假阳性(False Positive) 。
结论:有,是可能有;无,是肯定无。
核心短板:无法安全删除
标准的布隆过滤器不支持删除元素。因为多个元素可能会共享同一个位。如果简单地将某个位从1置为0来“删除”一个元素,可能会影响到其他共享该位的元素,导致查询它们时出现假阴性(False Negative) ——即元素明明存在,却被判断为不存在。这是布隆过滤器设计上绝对要避免的。
布隆过滤器的应用场景
正是基于其“快速、高效、有误判率、无假阴性”的特点,布隆过滤器在许多场景中大放异彩。
1. 解决缓存穿透
缓存穿透是指查询一个数据库和缓存中都不存在的数据。这种请求每次都会绕过缓存,直接打到数据库上。如果被恶意利用,高并发的穿透请求会像洪水一样冲垮数据库。
解决方案:
在缓存(如Redis)前再加一道布隆过滤器防线,将已存在数据的key存入其中。
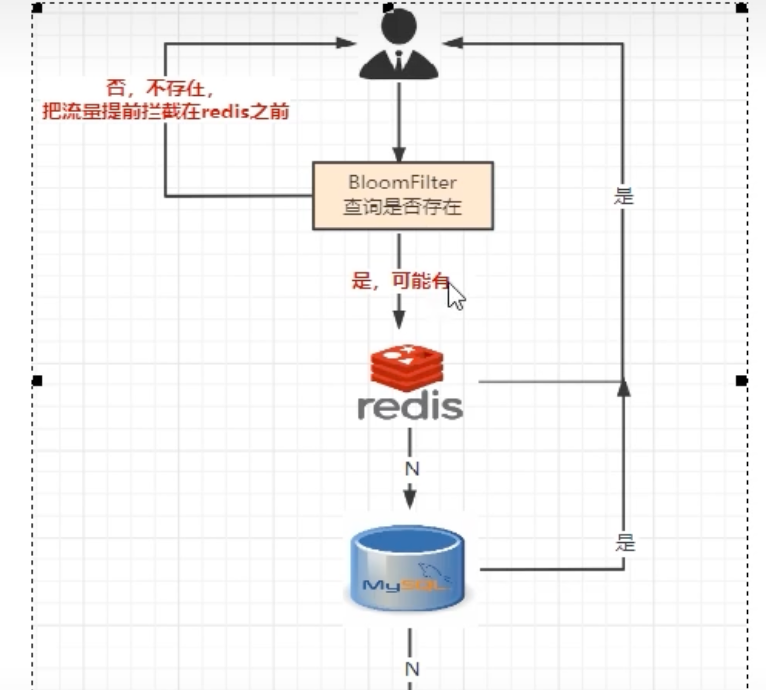
查询流程变为:
- 请求进来,先查询布隆过滤器。
- 如果过滤器判断key不存在,则直接返回,避免了后续对缓存和数据库的查询。
- 如果过滤器判断key可能存在,则继续查询缓存,若缓存未命中,再查询数据库。
这样,绝大多数对不存在数据的恶意查询在第一步就被拦截了,有效保护了后端系统。
2. 黑名单与垃圾邮件过滤
在全球数十亿的网址黑名单或垃圾邮件发信人列表中,判断一个URL或邮箱是否存在,布隆过滤器是绝佳方案。将所有黑名单项放入过滤器中,当收到请求或邮件时,先通过过滤器进行快速检测,高效拦截大部分恶意请求和垃圾邮件,只有在过滤器判断“可能存在”时,再进行更精确的校验。
布谷鸟过滤器 (Cuckoo Filter):支持删除的高性能继任者
布隆过滤器“无法删除”的特性在很多动态变化的场景下成为了一个痛点。为了解决这个问题,学术界在2014年的论文《Cuckoo Filter: Practically Better Than Bloom》中提出了布谷鸟过滤器。
参考文章:https://www.bluepuni.com/archives/cuckoo-filter/#cuckoo-hashing
1. 核心结构
布谷鸟过滤器由一个哈希表构成,表中的每个条目称为桶 (Bucket) ,每个桶内有多个槽 (Slot) 。过滤器存储的不是元素本身,而是元素的指纹 (Fingerprint) ——由元素哈希生成的一段短小的二进制串。
其设计的基石是:任何一个元素 x,都只可能被存放在两个候选桶中。这两个位置由两个独立的哈希函数 h1(x) 和 h2(x) 确定。
核心原则:一个元素的指纹,在任意时刻,仅会占据其两个候选桶中的一个槽位。查询时,也只需检查这两个桶。
2. 插入操作 (Insertion)
当插入一个新元素 x 时,系统会计算出其指纹 f 和两个候选桶的位置 i1 和 i2。
直接插入:检查桶
i1和i2是否有空槽。- 如果
i1有空槽,将指纹f放入其中,插入完成。 - 如果
i1已满,则检查i2。若i2有空槽,将f放入其中,插入完成。
- 如果
触发迁移:如果
i1和i2两个桶均已满,则必须腾出空间。这个过程即是布谷鸟过滤器著名的“鸠占鹊巢”机制:- 从
i1或i2中随机选择一个桶(例如i1)。 - 从
i1中随机驱逐一个已存在的指纹,记为f'。 - 将新指纹
f放入f'留出的空槽中。
- 从
3. 核心机制:确定性的迁移路径
现在,被驱逐的指纹 f' 变得“无家可归”,它必须被重新安置。它的新去向不是随机的,而是沿着一条完全确定的路径进行。
计算备用位置:每个指纹都有两个固定的候选位置。如果
f'是从它的位置p1被驱逐的,那么它唯一的备用位置就是p2。这个备用位置可以通过一个简单的异或运算(XOR)得出:
p2 = p1 ⊕ hash(f')这个公式确保了路径的确定性:知道当前位置和指纹,就能算出唯一的“另一个”位置。
连锁反应 (Cascading Relocation) :
- 被驱逐的指纹
f'移动到它的备用位置p2。 - 系统检查桶
p2是否有空槽。 - 若有空槽,将
f'放入,整个迁移过程结束。 - 若
p2 也已满,则f'会重复上述过程:从p2中再驱逐一个指纹f'',自己占据位置,然后f''接力进行迁移。
- 被驱逐的指纹
这个连锁迁移会一直持续,直到某个被驱逐的指纹找到了空槽,或者迁移次数达到了预设的上限(此时认为过滤器已满,插入失败)。
4. 查询与删除操作
- 查询 (Query) :计算元素
x的指纹f和两个候选桶i1,i2。只需在这两个桶的所有槽位中检查是否存在指纹f。如果任一位置存在,则元素可能存在;如果两处都不存在,则元素绝对不存在。 - 删除 (Deletion) :这是布谷鸟过滤器的优势所在。同样计算出
f、i1和i2。检查这两个桶,如果找到了指纹f,直接从槽位中将其移除即可。该操作是原子且安全的,不会影响任何其他元素。
布谷鸟过滤器 vs. 布隆过滤器
| 特性 | 布隆过滤器 (Bloom Filter) | 布谷鸟过滤器 (Cuckoo Filter) |
|---|---|---|
| 删除元素 | 不支持 | 原生支持,操作简单 |
| 空间效率 | 很高 | 通常更高 (在同等低误判率下) |
| 查询性能 | O(k),k为哈希函数个数 | O(1),仅需检查 2 个桶 |
| 插入性能 | O(k),稳定 | 均摊 O(1),但高负载下因迁移可能变慢 |
| 适用场景 | 数据集只增不减的场景,如防止缓存穿透、URL去重、垃圾邮件过滤。因其技术成熟、实现简单、性能稳定,在不需要删除元素的绝大多数场景下仍是首选。 | 需要频繁删除元素的动态数据集,如动态的IP黑名单、会话/令牌的有效性验证、跟踪滑动时间窗口内的独立访客等。 |
为什么布隆过滤器仍是主流选择?
既然布谷鸟过滤器在空间效率、查询性能和删除功能上看起来更优,为什么大多数公司和开源项目(如 Redis)还是默认使用或首先想到布隆过滤器?
主要原因有以下几点:
“不需要删除”的场景占绝大多数:
这是最根本的原因。在布隆过滤器最经典的几个应用场景中,删除操作本身就是一个伪需求。- 防止缓存穿透:我们用它来拦截那些不存在于数据库的 key。这个“不存在”的集合是动态增长的,但我们几乎没有“让一个不存在的 key 变得可以存在”的需求。通常的做法是定期重建布隆过滤器,而不是从中删除元素。
- 爬虫 URL 去重:爬虫系统判断一个 URL是否已经爬取过。这个已爬取的集合只会不断增加,不会减少。
- 推荐系统去重:过滤掉那些已经给用户推荐过的内容。这个集合同样是只增不减的。
简单性和稳定性:
布隆过滤器的算法原理和实现都非常简单:一个位数组和 k 个哈希函数。它的性能是稳定且可预测的,插入和查询的耗时都是 O(k),不会有“意外”。
相比之下,布谷鸟过滤器的插入操作在高负载(接近饱和) 时,可能会触发多次“踢出”和迁移操作,导致单次插入的耗时突然增加,性能出现抖动。对于需要严格控制延迟的系统来说,这种不确定性是一个需要考量的风险。技术惯性和生态成熟度:
布隆过滤器诞生于 1970 年,拥有几十年的应用历史,早已成为计算机科学领域的经典数据结构。各大主流语言都有成熟、稳定、经过大规模生产环境验证的库。而布谷鸟过滤器相对较新(2014年提出),虽然理论上很优秀,但其生态和社区的成熟度还需要时间积累。当工程师面临技术选型时,往往会倾向于更熟悉、更稳妥的“老朋友”。
scaling up:当亿级数据撑爆单个布隆过滤器
我们已经知道,布隆过滤器的位数组大小 m 取决于期望处理的元素数量 n 和可接受的误判率 p。当 n 达到十亿、百亿甚至更高量级时,即使误判率设置得相对宽松,计算出的位数组 m 也可能变得非常庞大,超出单台服务器的内存上限。例如,为一个10亿元素的集合设计一个误判率为 0.1% 的布隆过滤器,大约需要120亿个比特位,即1.5GB的内存。如果数据量再大十倍,这个数字就会变成15GB,开始触及普通服务器的内存瓶颈。
那么,当单个布隆过滤器大到无法在单机内存中容纳时,我们该如何应对?答案是:分布式和可伸缩设计。
1. 分布式布隆过滤器 (Distributed Bloom Filter)
核心思想很简单:将一个巨大的布隆过滤器水平切分,部署到多台机器上。这就像将一本超厚的字典拆分成A-G、H-P、Q-Z三卷,分给三个人保管。
实现方式:
最常见的方式是利用像 Redis 这样的分布式缓存系统。我们可以将一个大的 bit array 抽象地看作一个 key,然后将它分布到 Redis 集群的多个节点上。
查询流程:
客户端/协调节点:接收到要查询的元素
key。计算哈希:在客户端或协调节点上,使用
k个哈希函数计算出k个位数组的索引位置。路由请求:协调节点根据这些索引位置,判断它们分别属于哪个分片(哪个 Redis 节点)。
并行查询:向所有相关的 Redis 节点并行发送
GETBIT命令,检查对应位置的比特值。结果聚合:
- 只要有一个节点返回
0,协调节点就可以立即判定该元素绝对不存在。 - 必须所有相关节点都返回
1,协调节点才能判定该元素可能存在。
- 只要有一个节点返回
这种分片策略有效地将存储和计算压力分散到整个集群,实现了水平扩展。
2. 可伸缩布隆过滤器 (Scalable Bloom Filter)
分布式方案解决了“存不下”的问题,但它仍然需要预估数据总量来创建过滤器。如果数据量是持续增长、无法预估的呢?频繁地从零开始重建一个更大的分布式过滤器成本极高。
可伸缩布隆过滤器正是为此而生。它不是一个单一的过滤器,而是一个由多个布隆过滤器组成的链条。
工作原理:
初始化:开始时只有一个较小的布隆过滤器(我们称之为
BF1)。动态增长:当
BF1中添加的元素过多,导致其误判率即将超过预设的阈值时,系统会自动创建一个新的、通常容量更大的布隆过滤器BF2,并将其链接在BF1之后。插入:所有新来的元素总是被添加到最新的过滤器中(即
BF2)。查询:查询一个元素时,需要从最新的过滤器 (
BF2) 开始,向前逐一检查。- 如果在任何一个过滤器中(例如
BF2)被判断为“绝对不存在”,则立即返回结果,无需再查更旧的过滤器。 - 只有当查询的元素在所有过滤器中都被判断为“可能存在”时,最终结果才是“可能存在”。
- 如果在任何一个过滤器中(例如
这种设计确保了整体的误判率可以被控制在一个可接受的范围内,同时允许系统在不中断服务的情况下,平滑地适应无限增长的数据量。
结论
面对海量数据的存在性判断问题,布隆过滤器以其卓越的空间和时间效率提供了一个经典的解决方案,特别适用于静态数据集或允许少量误判的场景。而布谷鸟过滤器的出现,则解决了布隆过滤器无法删除元素的痛点,为需要动态增删的场景提供了更优的选择。